Geometry

Geometry was defined as an exposition of form proceeding from observation. It was also a very common means of demonstration among philosophers, who, “to adduce at once the most full-toned evidence, declare that their Jupiter made use of geometry in his works, when Jupiter engraved upon the vault of the skies precisely what the philosophers themselves drew in the sands of the earth. When this in a proper manner is transferred to our Almighty Creator, this assumption may then perhaps approach the truth.
The Holy Trinity makes use of geometry in so far as it bestows manifold forms and images upon the creatures which up to the present day it has called into being, as in its adorable omnipotence it further determines the course of the stars, as it prescribes their courses to the planets and as it assigns to the fixed stars their unalterable position. For every excellent and well-ordered arrangement can be reduced to the special requirement of this science. This science found realisation also at the building of the tabernacle and the temple; the same measuring rod, circles, spheres, hemispheres, quadrangles, and other figures were employed.
The knowledge of all this brings to him, who is occupied with it, no small gain for his spiritual culture.”
Euclid’s 47th Proposition
All Past Master’s collar and most Past Master’s jewels are engraved with a peculiar pattern, that being a right angled triangle with perfect squares upon its sides. This
“In right-angled triangles the square on the side opposite the right angle equals the sum of the squares on the sides containing the right angle.”

The proposition, I.47, is often called the Pythagorean theorem, called so by Proclus and others centuries after Pythagoras and even centuries after Euclid. The statement of the proposition was very likely known to the Pythagoreans if not to Pythagoras himself. The Pythagoreans and perhaps Pythagoras even knew a proof of it. But the knowledge of this relation was far older than Pythagoras.
More than a millennium before Pythagoras, the Old Babylonians (c.1900 BCE) used this relation to solve geometric problems involving right triangles. Moreover, the tablet known as Plimpton 322 shows that the Old Babylonians could construct all the so-called Pythagorean triples, those triples of numbers a, b, and c such that a2 + b2 = c2 which describe triangles with integral sides. (The smallest of these being 3, 4, 5.)
Proof
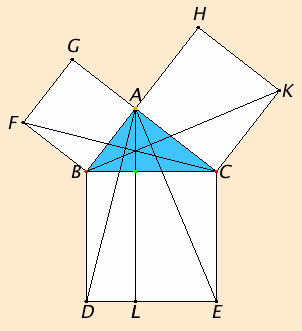
Let ABC be a right-angled triangle having the angle BAC right. It is proposed that the square on BC equals the sum of the squares on BA and AC.
Describe the square BDEC on BC, and the squares GB and HC on BA and AC. Draw AL through A parallel to either BD or CE and join AD and FC.
Since each of the angles BAC and BAG is right, it follows that with a straight line BA, and at the point A on it, the two straight lines AC and AG not lying on the same side make the adjacent angles equal to two right angles, therefore CA is in a straight line with AG. For the same reason BA is also in a straight line with AH.
Since the angle DBC equals the angle FBA, for each is right, add the angle ABC to each, therefore the whole angle DBA equals the whole angle FBC.
Since DB equals BC, and FB equals BA, the two sides AB and BD equal the two sides FB and BC respectively and the angle ABD equals the angle FBC, therefore the base AD equals the base FC, and the triangle ABD equals the triangle FBC.
Now the parallelogram BL is double the triangle ABD, for they have the same base BD and are in the same parallels BD and AL. Also the square GB is double the triangle FBC, for they again have the same base FB and are in the same parallels FB and GC. Therefore the parallelogram BL also equals the square GB.
Similarly, if AE and BK are joined, the parallelogram CL can also be proved equal to the square HC. Therefore the whole square BDEC equals the sum of the two squares GB and HC and the square BDEC is described on BC, and the squares GB and HC on BA and AC.
Therefore the square on BC equals the sum of the squares on BA and AC. Therefore “in right-angled triangles the square on the side opposite the right angle equals the sum of the squares on the sides containing the right angle”.
![]()
